
Helling van een lijnformule en vergelijkingen, representatie, voorbeelden
De helling van een lijn is de raaklijn van de hoek θ die de lijn vormt met de horizontale as, die volgens afspraak tegen de klok in wordt gemeten. De helling van elke lijn is altijd constant en daarom is het een van de meest essentiële kenmerken..
Om het te berekenen, moet u twee punten op de lijn kennen, waarvan de coördinaten (x1,Y1) en (xtwee,YtweeTussen beide punten wordt een segment getekend dat bij de lijn hoort en vervolgens worden de segmenten getekend die de afstand tussen x vertegenwoordigen.1 en xtwee, en tussen en1 en entwee, zoals in de onderstaande afbeelding.
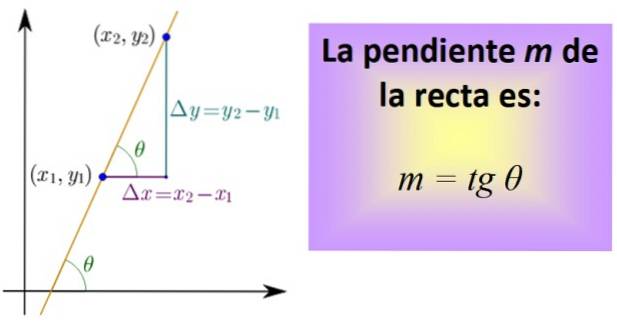
De drie segmenten vormen een rechthoekige driehoek waarvan de benen zijn: Δx = xtwee - X1 y Δy = ytwee - Y1. Ze komen overeen met respectievelijk een horizontale en een verticale verplaatsing..
Nu definiëren we een quotiënt, genaamd de tangens van de hoek θ en afgekort tg θ, wat precies de helling is m van het rechte stuk:
m = tg θ = Δy / Δx
Merk op dat voor een lijn deze hoek constant blijft, ongeacht de punten die zijn genomen om de raaklijn te berekenen. Deze waarde geeft ons in ieder geval een maat voor hoe steil de lijn is.
Door de coördinaten van de geselecteerde punten is de formule voor de helling:
m = (y - y1 ) / (xtwee - X1
Artikel index
- 1 Grafische weergave
- 2 soorten hellingen
- 3 Hoe bereken je de helling van een lijn?
- 4 Opgeloste oefeningen
- 4.1 - Oefening 1
- 4.2 - Oefening 2
- 5 voorbeelden
- 5.1 Voorbeeld 1
- 5.2 Voorbeeld 2
- 6 referenties
Grafische voorstelling
Hieronder hebben we verschillende situaties waarin het concept van helling relevant is. De waarde ervan kan eenvoudig worden berekend door de respectieve verticale en horizontale verplaatsing te meten en vervolgens het quotiënt te maken dat aan het begin wordt aangegeven.
Dit geeft ons een idee van de oneffenheid of achteruitgang van een constructie, zoals een hellingbaan, een dak of een weg:
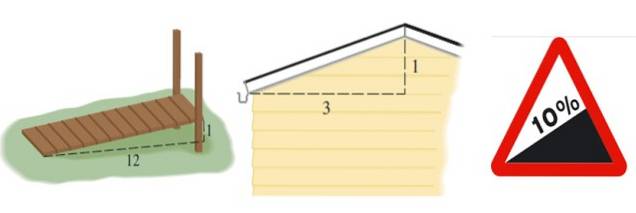
De helling van de oprit in figuur 2 links is m = 1/12, die van het dak is m = 1/3 en die van de weg wordt uitgedrukt in een percentage. Een percentage van 10% betekent dat voor elke 100 meter die horizontaal voortschrijdt, 10 meter hoogte wordt gewonnen:
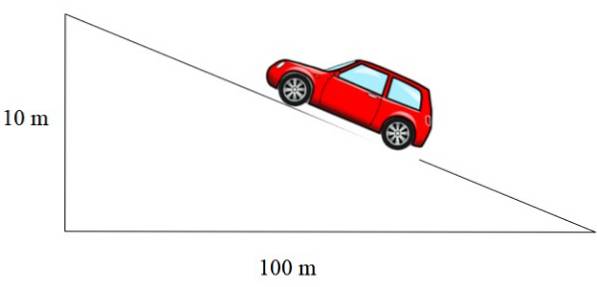
In dit geval is de helling 10/100 = 0,1, wat, uitgedrukt als een percentage, gelijk is aan 10%..
Soorten pistes
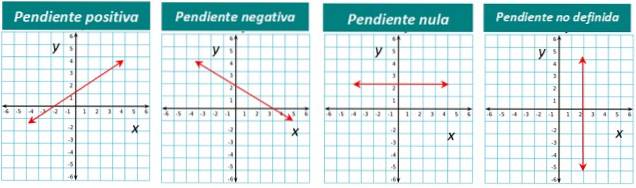
De helling van een lijn kan positief, negatief of nul zijn. De lijn in figuur 1 heeft bijvoorbeeld een positieve helling. We waarderen het meteen omdat we zien dat de lijn "stijgt" als we hem van links naar rechts zien.
Als de lijn van links naar rechts daalt, is de helling negatief. En als een lijn horizontaal is, is de helling nul.
Ten slotte is voor verticale lijnen de helling niet gedefinieerd.
De grafische weergave van elk type is hieronder:
Hoe bereken je de helling van een lijn?
Het berekenen van de helling is heel eenvoudig, je hoeft alleen de verticale verplaatsing en de horizontale verplaatsing te vinden en vervolgens het quotiënt tussen beide te maken.
Als we de tekening van de lijn in het cartesische vlak hebben, worden deze verplaatsingen gevonden door twee willekeurige punten op de lijn P te kiezen1 En Ptwee, de coördinaten bepalen en de aan het begin gegeven definitie toepassen:
m = (y - y1 ) / (xtwee - X1
Omdat de waarde van de helling onafhankelijk is van de keuze van P1 En Ptwee , we gaan een punt P kiezen uit een van de coördinaten (x, y) dat bij de lijn hoort, waarvan de coördinaten niet bekend zijn, en een ander punt P1 waarvan de coördinaten zijn: (x1,Y1.
De helling is:
m = (y - y1) / (x - x1
We kunnen de Y
en en1 = m (x - x1
Stel nu dat punt P1 is het snijpunt van de lijn met de verticale as, van coördinaten (0, b). Vervang dit in de bovenstaande vergelijking:
y - b = m (x - 0) → y = mx + b
Deze uitdrukking staat bekend als de vergelijking van de lijn in het formulier helling - onderscheppen, aangezien de lijn ondubbelzinnig wordt bepaald wanneer de helling en het snijpunt met de verticale as bekend zijn.
Alleen de helling kennen is niet voldoende om een lijn in het vlak te karakteriseren, aangezien oneindige lijnen dezelfde helling kunnen hebben, wat betekent dat ze parallel zijn, maar door andere punten gaan.
Opgeloste oefeningen
- Oefening 1
Zoek de helling van de lijn die wordt weergegeven in de volgende afbeelding:
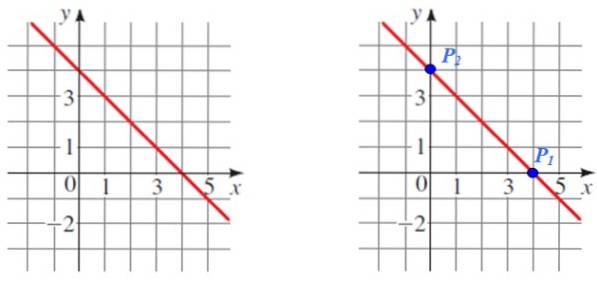
Oplossing
P.1 En Ptwee zijn twee gemakkelijk te lezen punten die zullen worden gebruikt voor de berekening, merk ook op dat het de respectieve snijpunten zijn met de coördinaatassen.
De coördinaten van elk punt zijn:
P.1 (4.0) en Ptwee (0,4)
Door in de vergelijking de helling te vervangen:
m = (4 - 0) / (0 - 4) = 4 / (- 4) = -1
De helling is negatief, wat te verwachten was na het bekijken van de grafiek.
- Oefening 2
Zoek de vergelijking van de lijn die door het punt (1, -6) gaat en evenwijdig is aan de lijn y = 2x - 3.
Oplossing
De helling van de gezochte lijn moet dezelfde zijn als die van y = 2x - 3, aangezien ze parallel zijn. Voor deze lijn is de helling m = 2, daarom heeft degene die we zoeken de vorm:
en en1 = 2 (x - x1
Nu vervangen we het punt waar onze lijn doorheen gaat: x1 = 1 en y1 = -6.
y - (-6) = 2 (x - 1)
Daarom y = 2x - 2 - 6 → y = 2x - 8
Voorbeelden
Twee grootheden kunnen zo met elkaar in verband worden gebracht dat hun grafiek een rechte lijn is. In dat geval wordt gezegd dat de grootheden lineaire afhankelijkheid hebben en dat de helling van de lijn kan worden geïnterpreteerd als de mate van verandering van de ene variabele naar de andere.
voorbeeld 1
Stel dat een zwembad is gevuld met water bij a tarief constant in de tijd. Hoe meer tijd verstrijkt, hoe meer water er natuurlijk wordt opgeslagen. Welnu, de snelheid waarmee het zwembad wordt gevuld, is precies de helling van de lijn die het volume relateert aan de tijd:
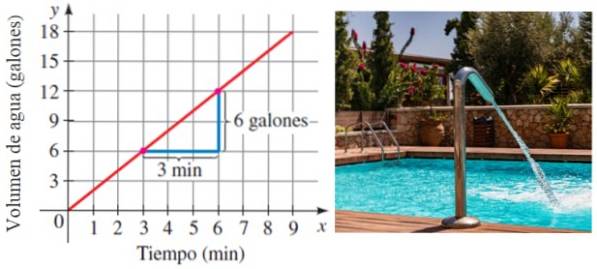
In dit voorbeeld vult het zwembad zich met een snelheid van 6/3 gallon per minuut of 2 gallon / minuut.
Voorbeeld 2
Wanneer een mobiel met constante snelheid in een rechte lijn beweegt, is de helling van de positiegrafiek als functie van de tijd niets anders dan genoemde snelheid. De grafiek toont een mobiel met een positieve snelheid, wat betekent dat hij van de oorsprong af beweegt.
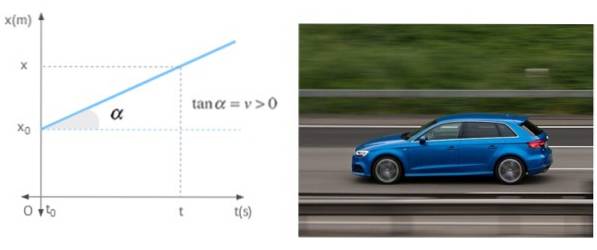
Referenties
- Alvarez, J. De helling van een snelweg. Hersteld van: geogebra.es.
- Carena, M. 2019. Pre-University Mathematics Manual. Nationale Universiteit van de Litoral.
- Hoffman, J. Selectie van wiskundeonderwerpen. Deel 4.
- Jiménez, R. 2008. Algebra. Prentice hal.
- Stewart, J. 2006. Precalculus: wiskunde voor calculus. 5e. Editie. Cengage leren.
- Zill, D. 1984. Algebra en trigonometrie. Mcgraw heuvel.



Niemand heeft nog op dit artikel gereageerd.