
Regelmatige polygonen eigenschappen, elementen, hoeken, voorbeelden
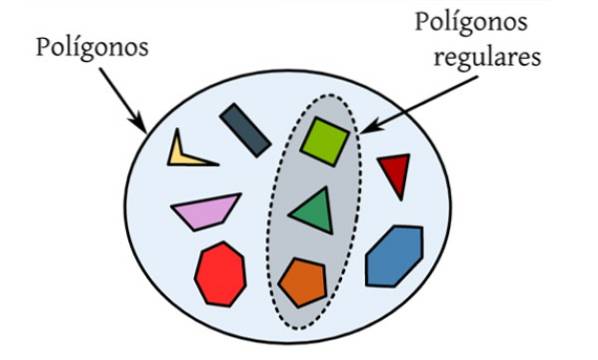
De regelmatige veelhoeken zijn degenen die al hun zijden en hun interne hoeken gelijk hebben. In de volgende afbeelding is er een reeks verschillende polygonen, dit zijn vlakke figuren die worden begrensd door een gesloten curve en alleen degene die zijn gemarkeerd, voldoen aan de voorwaarden om regelmatig te zijn.
De gelijkzijdige driehoek is bijvoorbeeld een regelmatige veelhoek, aangezien de drie zijden hetzelfde meten, evenals de interne hoeken, die elk 60 ° waard zijn..
Het vierkant is een vierhoek met vier even grote zijden en waarvan de interne hoeken 90º zijn. Het wordt gevolgd door de regelmatige vijfhoek, met vijf zijden van gelijke grootte en vijf interne hoeken van 108º elk..
Als een veelhoek regelmatig is, wordt dit woord toegevoegd aan de speciale naam, dus we hebben de regelmatige zeshoek, de regelmatige zevenhoek enzovoort.
Artikel index
- 1 Eigenschappen van regelmatige veelhoeken
- 2 Elementen van een regelmatige veelhoek
- 2.1 Vertex
- 2.2 Zijkant
- 2.3 Diagonaal
- 2.4 Centrum
- 2.5 Radio
- 2.6 Apothema
- 2.7 Centrale hoek
- 2.8 Sagita
- 3 Omtrek en oppervlakte
- 3.1 Omtrek
- 3.2 Gebied
- 4 hoeken
- 4.1 Centrale hoek
- 4.2 Binnenhoek of binnenhoek
- 4.3 Externe hoeken
- 5 Voorbeelden van regelmatige veelhoeken
- 5.1 - Regelmatige veelhoeken in het dagelijks leven en de natuur
- 5.2 - Regelmatige zeshoeken in de natuur
- 6 Oefening opgelost
- 6.1 Oplossing
- 7 referenties
Eigenschappen van regelmatige veelhoeken
De belangrijkste eigenschappen van regelmatige polygonen kunnen als volgt worden samengevat:
-De zijkanten zijn hetzelfde, dus ze zijn gelijkzijdig.
-Zij zijn gelijkhoekig, omdat al zijn interne hoeken dezelfde maat hebben.
-Ze kunnen altijd in een omtrek worden gegraveerd, wat betekent dat ze perfect passen binnen één, die wordt genoemd omgeschreven omtrek.
-Voor een regelmatige veelhoek met n zijden is de maat van een binnenhoek α:
a = [180 (n-2)] / n
-Je kunt n (n-3) / 2 diagonalen tekenen vanuit de hoekpunten van een veelhoek, of deze nu regelmatig is of niet.
-De som van de buitenhoeken is gelijk aan 360º.

Elementen van een regelmatige veelhoek
Vervolgens presenteren we de belangrijkste elementen van een regelmatige veelhoek, weergegeven in de onderstaande afbeelding.

Vertex
Gemeenschappelijk punt dat twee opeenvolgende zijden hebben, aangegeven als V in de figuur.
Kant
Het is het segment dat twee opeenvolgende hoekpunten van de veelhoek verbindt en wordt aangeduid als ℓ of L.
Diagonaal
Segment dat twee niet-opeenvolgende hoekpunten van de veelhoek verbindt, in de figuur wordt het aangeduid als d.
Centrum
Het is het gemeenschappelijke middelpunt van de ingeschreven cirkel en de omgeschreven cirkel, aangeduid met de letter O. Het kan ook worden gezien als het enige punt op gelijke afstand van zowel de hoekpunten als de middelpunten van elke zijde..
Radio
Het is de radio r van de omgeschreven cirkel en valt samen met de afstand tussen O en een hoekpunt.
Apothem
Het heet apothema naar de straal van de omtrek ingeschreven in de veelhoek, weergegeven in de figuur met een letter naar. De apothema staat loodrecht op één kant en verbindt deze met de middelste O (rood segment in figuur 3).
Als we de straal r en de lengte van de zijkant kennen, wordt de apothema berekend door:
Omdat de apothema in feite een van de benen van een rechthoekige driehoek is (zie figuur 3), heeft het andere been de waarde ℓ / 2 (de helft van een zijde) en de hypotenusa de straal r van de veelhoek.
Wanneer de stelling van Pythagoras op deze driehoek wordt toegepast, wordt deze vergelijking verkregen, die niet alleen geldig is voor de zeshoek, maar voor elke regelmatige veelhoek..
Centrale hoek
Het is de hoek waarvan het hoekpunt samenvalt met het middelpunt O en waarvan de zijkanten de segmenten zijn die het midden verbinden met twee opeenvolgende hoekpunten. Zijn maat in sexagesimale graden is 360º / n, waar n is het aantal zijden van de veelhoek.
Sagita
Het is het verschil tussen de straal van de veelhoek en de apothema (zie figuur 3). De sagitta aanduiden als S:
S = r - een
Omtrek en gebied
Omtrek
Het is gemakkelijk te berekenen door de lengtes van de zijkanten op te tellen. Aangezien elke zijde dezelfde lengte L heeft en er n zijden zijn, wordt de omtrek P uitgedrukt als:
P = n.L
Oppervlakte
In een regelmatige veelhoek wordt het gebied A gegeven door het product tussen de halve omtrek (de helft van de omtrek) en de lengte van de apothema naar.
A = P.a / 2
Omdat de omtrek afhangt van het aantal zijden n, blijkt dat:
A = (nL). Een / 2
Twee regelmatige polygonen kunnen dezelfde omtrek hebben, zelfs als ze niet hetzelfde aantal zijden hebben, omdat dit dan afhangt van de lengte van de zijden.
In boek V van hem Verzameling, de wiskundige Pappus van Alexandrië (290-350), de laatste van de grote oude Griekse wiskundigen, toonde aan dat van alle regelmatige polygonen met dezelfde omtrek, degene met de grootste oppervlakte degene is met het grootste aantal zijden.
Hoeken
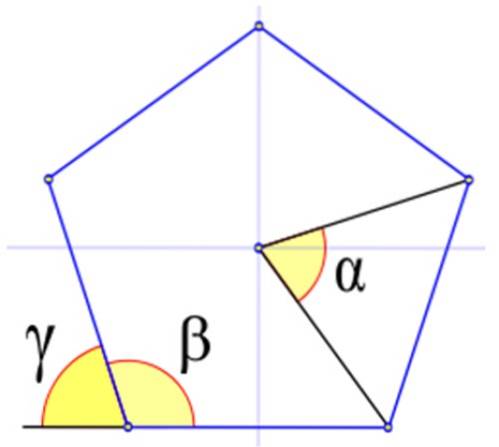
Figuur 4 toont de relevante hoeken in een regelmatige veelhoek, aangeduid met de Griekse letters α, β en γ.
Centrale hoek
Eerder noemden we de centrale hoek, tussen de elementen van de regelmatige veelhoek, het is de hoek waarvan het hoekpunt in het midden van de veelhoek ligt en de zijkanten zijn de segmenten die het midden verbinden met twee opeenvolgende hoekpunten.
Om de maat van de centrale hoek α te berekenen, deelt u 360º door n, het aantal zijden. Of 2π radialen tussen n:
α = 360º / n
Equivalent in radialen aan:
α = 2π / n
Binnenhoek of binnenhoek
In figuur 4 is de interne hoek β degene waarvan de top samenvalt met een van de figuur en de zijkanten zijn ook zijden van de figuur. Het wordt berekend in sexagesimale graden door:
p = [180 (n-2)] / n
Of in radialen met:
β = [π (n-2)] / n
Externe hoeken
Ze worden aangeduid met de Griekse letter γ. De figuur laat zien dat γ + β = 180º. Daarom:
γ = 180º - β
De som van alle externe hoeken op een regelmatige veelhoek is 360 °.

Voorbeelden van regelmatige veelhoeken
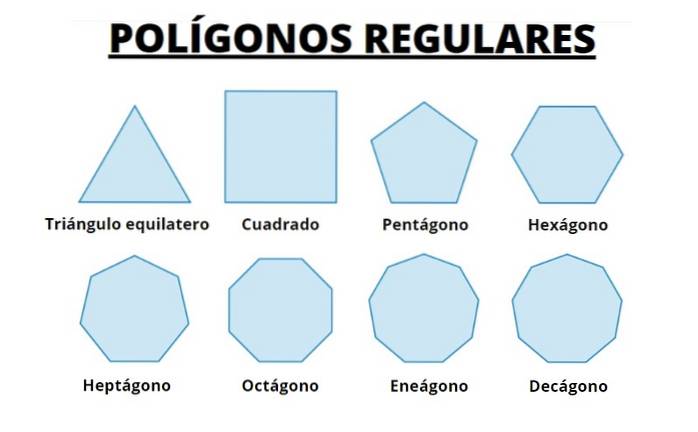
Vervolgens hebben we de eerste 8 regelmatige polygonen. We zien dat naarmate het aantal zijden toeneemt, de veelhoek steeds meer lijkt op de omtrek waarin ze zijn ingeschreven.
We kunnen ons voorstellen dat door de lengte van de zijkanten kleiner en kleiner te maken, en het aantal hiervan te vergroten, we de omtrek krijgen.
- Regelmatige veelhoeken in het dagelijks leven en de natuur
Regelmatige veelhoeken komen overal in het dagelijks leven en zelfs in de natuur voor. Laten we eens kijken naar enkele voorbeelden:
Verkeerssignalen
Regelmatige polygonen zoals gelijkzijdige driehoeken, vierkanten en ruiten zijn er in overvloed in de bewegwijzering die we op snelwegen en wegen zien. In figuur 6 zien we een stopbord met een achthoekige vorm.

Meubilair
Talloze meubelstukken hebben bijvoorbeeld het vierkant als hun karakteristieke geometrische figuur, net zoals veel tafels, stoelen en banken vierkant zijn. Een parallellepipedum is over het algemeen een doos met zijden in de vorm van een rechthoek (wat geen regelmatige veelhoek is), maar ze kunnen ook vierkant gemaakt worden..
Architectuur en constructie
De tegels op vloeren en muren, zowel in huizen als op straat, hebben vaak de vorm van regelmatige veelhoeken..
Tessellations zijn oppervlakken die volledig zijn bedekt met tegels die verschillende geometrische vormen hebben. Met de driehoek, het vierkant en de zeshoek kun je regelmatige vlakverdelingen maken, diegene die slechts één type figuur gebruiken om perfect te bedekken, zonder lege ruimtes te laten (zie figuur 6).
Evenzo maken gebouwen gebruik van regelmatige polygonen in elementen zoals ramen en decoratie..

- Regelmatige zeshoeken in de natuur
Verrassend genoeg is de regelmatige zeshoek een veelhoek die vaak in de natuur voorkomt..
De kammen die door bijen worden gemaakt om honing op te slaan, hebben de vorm van een regelmatige zeshoek. Zoals Pappus van Alexandrië opmerkte, optimaliseren de bijen op deze manier de ruimte om zoveel mogelijk honing op te slaan..
En er zijn ook regelmatige zeshoeken in de schaal van de schildpadden en de sneeuwvlokken, die ook verschillende zeer mooie geometrische vormen aannemen..
Oefening opgelost
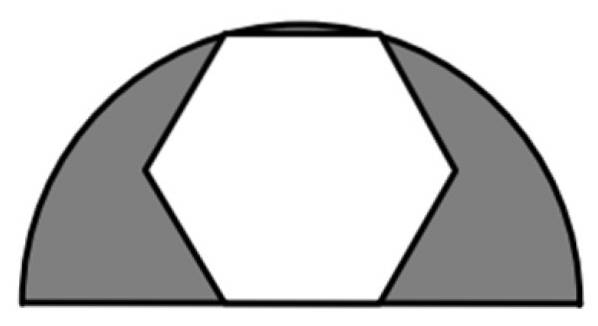
Een regelmatige zeshoek is ingeschreven in een halve cirkel met een straal van 6 cm, zoals weergegeven in de figuur. Wat is de waarde van het gearceerde gebied?
Oplossing
Het gearceerde gebied is het verschil tussen het gebied van de halve cirkel met straal R = 6 cm en het gebied van de gehele zeshoek, een regelmatige zeskantige veelhoek. We hebben dus formules nodig voor de oppervlakte van elk van deze figuren.
Halve cirkel gebied
NAAR1 = π Rtwee / 2 = π (6 cm)twee / 2 = 18π cmtwee
Regelmatig zeshoekig gebied
De formule om de oppervlakte van een regelmatige veelhoek te berekenen is:
A = P.a / 2
Waar P. is de omtrek en naar is de apothema. Omdat de omtrek de som van de zijden is, hebben we de waarde hiervan nodig. Voor de gewone zeshoek:
P = 6ℓ
Daarom:
A = 6ℓa / 2
Om de waarde van de zijde ℓ te vinden, is het nodig om hulpfiguren te construeren, die we hieronder zullen toelichten:
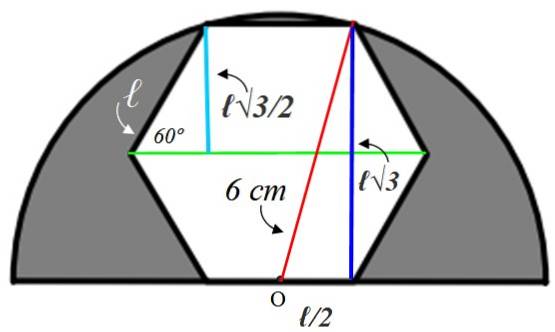
Laten we beginnen met de kleine rechthoekige driehoek aan de linkerkant, waarvan de hypotenusa ℓ is. Een interne hoek van de zeshoek is gelijk aan:
α = [180 (n-2)] / n = α = [180 (6-2)] / 6 = 120º
De straal die we in groen hebben getekend, doorsnijdt deze hoek, daarom is de scherpe hoek van de kleine driehoek 60º. Met de verstrekte informatie wordt deze driehoek opgelost door de lichtblauwe zijde te vinden, die hetzelfde meet als de apothema:
Tegenover been = a = ℓ x sin 60º = ℓ√3 / 2 cm
Deze waarde het is het dubbele van de donkerblauwe poot van de grote driehoek aan de rechterkant, maar uit deze driehoek weten we dat de hypotenusa 6 cm meet omdat dit de straal is van de halve cirkel. Het resterende been (onderkant) is gelijk aan ℓ / 2 aangezien punt O in het midden van de zijkant ligt.
Omdat de binnenhoeken van deze driehoek niet bekend zijn, kunnen we er de stelling van Pythagoras voor stellen:
36 = 3 ℓtwee + ℓtwee / 4
(13/4) ℓtwee = 36 → ℓ = √ (4 x36) / 13 cm = 12 / √13 cm
Met deze waarde wordt de apothema berekend:
a = ℓ√3 / 2 cm = (12 / √13) x (√3 / 2) cm = 6√3 / √13 cm
Laten we bellentwee naar het gebied van de regelmatige zeshoek:

= 28,8 cmtwee
Gearceerd figuurgebied
NAAR1 - NAARtwee = 18π cmtwee - 28,8 cmtwee = 27,7 cmtwee
Referenties
- Baldor, A. 1973. Meetkunde en driehoeksmeting. Centraal-Amerikaanse culturele uitgeverij.
- Geniet van wiskunde. Tessellations. Hersteld van: gustolasmatematicas.com.
- E. A. 2003. Geometrie-elementen: met oefeningen en kompasgeometrie. Universiteit van Medellin.
- Zeshoeken in de natuur. Hersteld van: malvargamath.wordpress.com.
- Jiménez, R. 2010. Wiskunde II. Geometrie en trigonometrie. Tweede druk. Prentice hal.
- Regelmatige veelhoeken. Hersteld van: mate.ingenieria.usac.edu.gt.
- Wikipedia. Apothem. Hersteld van: es.wikipedia.org.



Niemand heeft nog op dit artikel gereageerd.