De cartografische kegelsnede projectie Het wordt gekenmerkt door het projecteren van de punten van een bolvormig oppervlak op het oppervlak van een kegel, waarvan de top zich bevindt op de as die door de polen gaat en de bol raakt of secans. De kegel is een oppervlak dat in een vlak kan worden geopend, een hoeksector vormt en zonder de daarop geprojecteerde lijnen te vervormen.
De wiskundige Johann Heinrich Lambert (1728-1777) was degene die deze projectie bedacht, die voor het eerst in zijn boek verscheen Freye perspectief (1759), waar hij verschillende theorieën en reflecties over projecties samenstelde.
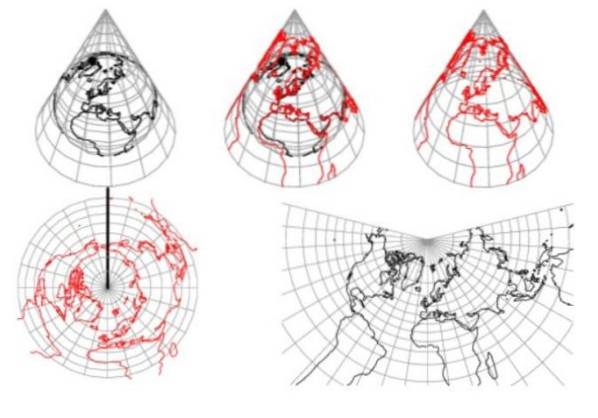
In de kegelvormige projecties van het aardoppervlak worden de meridianen radiale lijnen gecentreerd op het hoekpunt, met gelijke hoekafstanden, en worden de aardse parallellen cirkelvormige bogen concentrisch met het hoekpunt..
Figuur 1 laat zien dat het kegelvormige uitsteeksel het niet mogelijk maakt om beide hemisferen weer te geven. Bovendien wordt duidelijk opgemerkt dat de afstanden worden vervormd weg van de parallellen die de kegel onderscheppen.
Om deze redenen wordt dit type projectie gebruikt om gebieden van gemiddelde breedtegraad, uitgestrekt van oost naar west en van mindere noord-zuid-omvang weer te geven. Dat is het geval in de continentale Verenigde Staten.
Artikel index
De aarde kan worden benaderd tot een bol met een straal van 6378 km, gezien het feit dat alle land- en watermassa's zich op die grote bol bevinden. Het gaat erom dit oppervlak, dat een object in drie dimensies bedekt, zoals een bol, om te zetten in een ander object in twee dimensies: een platte kaart. Dit brengt het ongemak met zich mee dat het gekromde oppervlak vervormd wordt wanneer men het op het vlak wil projecteren.
Kaartprojecties, zoals de kegelvormige projectie, proberen dit probleem op te lossen met zo min mogelijk verlies aan nauwkeurigheid. Daarom zijn er verschillende opties om een projectie te maken, afhankelijk van de kenmerken die u wilt benadrukken..
Tot deze belangrijke kenmerken behoren afstanden, oppervlakte, hoeken en meer. De beste manier om ze allemaal te behouden, is door de aarde op schaal in 3D weer te geven. Maar dit is niet altijd praktisch.
Een wereldbol overal mee naartoe nemen is niet eenvoudig, omdat het volume in beslag neemt. Je kunt ook niet het hele aardoppervlak tegelijk zien, en het is onmogelijk om alle details op een schaalmodel weer te geven..
We kunnen ons voorstellen dat de planeet een sinaasappel is, we schillen de sinaasappel en spreiden de schil over de tafel, in een poging het beeld van het oppervlak van de sinaasappel te reconstrueren. Het is duidelijk dat daarbij veel informatie verloren gaat.
De projectie-opties zijn als volgt:
- Projecteer op een vliegtuig of
- Op een cilinder, die ontwikkeld kan worden als een rechthoekig vlak.
- Eindelijk op een kegel.
Het conische projectiesysteem heeft het voordeel dat het exact over de gekozen parallellen gaat om de projectiekegel te onderscheppen..
Bovendien houdt het de oriëntatie langs de meridianen praktisch intact, hoewel het de schaal langs de meridianen enigszins kan verstoren voor breedtegraden die ver verwijderd zijn van standaard- of referentieparallellen. Daarom is het passend om zeer grote landen of continenten te vertegenwoordigen.
Het is het kegelvormige projectiesysteem dat oorspronkelijk werd gebruikt door Ptolemaeus, een Griekse geograaf die leefde tussen 100-170 na Christus. Later in 1745 werd het verbeterd.
Het wordt vaak gebruikt in de atlassen van regio's met tussenliggende breedtegraden. Het is geschikt voor het weergeven van gebieden met een paar breedtegraden die tot een van de equatoriale hemisferen behoren.
Bij deze projectie zijn de afstanden waar langs de meridianen en in de twee standaardparallellen, dat wil zeggen de parallellen die zijn gekozen om te onderscheppen met de projectiekegel..
In de equidistante kegelvormige projectie strekt een punt op de bol zich radiaal uit tot het snijpunt met de raaklijn of secanskegel, waarbij het midden van de bol als het middelpunt van projectie wordt genomen.
Nadelen
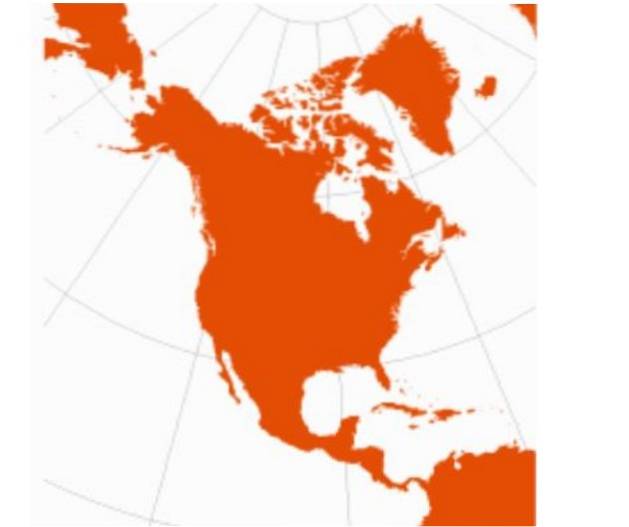
Het grootste nadeel van de kegelsnede uitsteeksel is dat deze niet toepasbaar is op equatoriale gebieden.
Bovendien is de kegelvormige projectie niet geschikt voor het in kaart brengen van grote regio's, maar eerder voor bepaalde gebieden, zoals Noord-Amerika..
Gebruik twee standaardparallellen en behoud het gebied, maar niet de schaal en vorm. Dit type kegelvormige projectie werd in 1805 geïntroduceerd door H.C. Albers.
Alle gebieden op de kaart zijn evenredig met die op aarde. In beperkte regio's zijn de richtingen relatief nauwkeurig. De afstanden komen overeen met die van het bolvormige oppervlak op de standaardparallellen.
In de Verenigde Staten wordt dit projectiesysteem gebruikt voor kaarten die de grenzen van de staten van de Unie aangeven, waarvoor 29,5 ° N en 45,5 ° N zijn gekozen als standaardparallellen, wat resulteert in een maximale schaalfout van 1, 25%.
Kaarten gemaakt met deze projectie behouden niet de hoeken die overeenkomen met die van de bol, noch bewaren ze perspectief of equidistantie.
Het werd in 1772 voorgesteld door de Zwitserse wiskundige en geograaf met dezelfde naam. Het belangrijkste kenmerk is dat het een kegel gebruikt die raakt aan of secans aan de bol en dat de projectie de hoeken onveranderlijk houdt. Deze eigenschappen maken het erg handig in luchtvaartnavigatiekaarten..
De United States Geological Survey (USGS) gebruikt de Lambert Conic-projectie. In deze projectie zijn de afstanden waar langs de standaardparallellen.
In de Lambert kegelsnede projectie blijven de richtingen redelijk nauwkeurig. De gebieden en vormen zijn enigszins vervormd op posities die dicht bij de standaardparallellen liggen, maar de verandering van vorm en gebied neemt toe naarmate ze van elkaar gescheiden zijn..
Omdat het doel van deze projectie is om richtingen en hoeken gelijk te houden aan de oorspronkelijke op de bol of ellipsoïde, is er geen geometrische methode om deze te verkrijgen, in tegenstelling tot de equidistante projectie van Ptolemaeus..
Het is eerder een analytische projectiemethode, gebaseerd op wiskundige formules.
De USGS-basiskaarten voor de 48 continentale staten gebruiken 33ºN en 45ºN als standaardparallellen, wat een maximale kaartfout oplevert van 2,5%..
Voor navigatiekaarten in Alaska zijn de gebruikte basisparallellen 55ºN en 65ºN. In plaats daarvan gebruikt de nationale atlas van Canada 49ºN en 77ºN.
Niemand heeft nog op dit artikel gereageerd.