De snijmodule beschrijft de reactie van een materiaal op de toepassing van een schuifspanning die het vervormt. Andere vaak gebruikte namen voor afschuifmodulus zijn afschuifmodulus, afschuifmodulus, transversale elasticiteit of tangentiële elasticiteit..
Als de spanningen klein zijn, zijn de vervormingen daarmee evenredig, volgens de wet van Hooke, waarbij de afschuifmodulus de constante van evenredigheid is. Daarom:
Afschuifmodulus = schuifspanning / rek
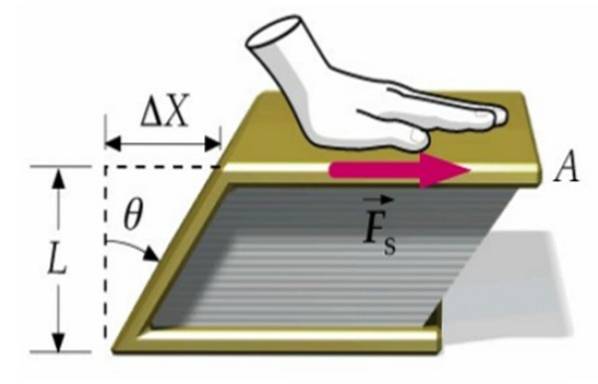
Stel dat de ene kracht op de omslag van een boek wordt uitgeoefend, de andere op het oppervlak van de tafel. Op deze manier beweegt het boek als geheel niet, maar vervormt het wanneer de bovenste omslag beweegt ten opzichte van de onderste met de hoeveelheid Ax.
Het boek gaat van een rechthoekige doorsnede naar een parallellogramvormige doorsnede, zoals we in de afbeelding hierboven zien.
Worden:
τ = F / A
De schuifspanning of spanning, zijn F. de grootte van de uitgeoefende kracht en NAAR het gebied waarop het inwerkt.
De veroorzaakte vervorming wordt gegeven door het quotiënt:
δ = Δx / L
Daarom is de afschuifmodulus, die we zullen aanduiden als G, is:
En aangezien Δx / L geen afmetingen heeft, zijn de eenheden van G hetzelfde als de schuifspanning, de verhouding tussen kracht en oppervlakte..
In het internationale systeem van eenheden zijn deze eenheden Newton / vierkante meter of pascal, afgekort Pa. En in Angelsaksische eenheden is het pond / vierkante inch, afgekort psi.
Artikel index
Onder invloed van afschuifkrachten zoals beschreven, bieden de objecten een weerstand die vergelijkbaar is met die van het boek, waarin de binnenste lagen verschuiven. Dit type vervorming kan alleen optreden bij vaste lichamen die voldoende stijf zijn om vervorming te weerstaan..
Aan de andere kant bieden vloeistoffen dit soort weerstand niet, maar ze kunnen volumevervormingen ondergaan.
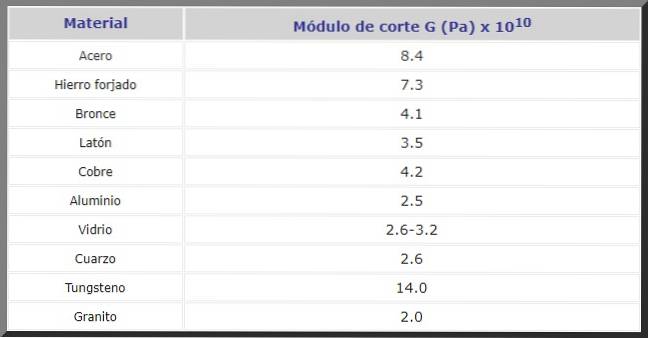
Hieronder vindt u de G in Pa-snijmodule voor verschillende materialen die vaak worden gebruikt in de bouw en bij de fabricage van machines en allerlei soorten reserveonderdelen:
Om de waarde van de afschuifmodulus te vinden, moeten monsters van elk materiaal worden getest en hun reactie op de toepassing van een schuifspanning moet worden onderzocht..
Het monster is een staaf gemaakt van het materiaal, met straal R en lengte L. bekend, die aan het ene uiteinde is bevestigd, terwijl het andere is verbonden met de as van een vrij te roteren katrol.
De katrol is vastgebonden met een touw, aan het vrije uiteinde waarvan een gewicht wordt opgehangen dat een kracht uitoefent F. op de staaf door het touw. En deze kracht produceert op zijn beurt een moment M. op de staaf, die dan een kleine hoek θ draait.
Een diagram van de montage is te zien in de volgende afbeelding:
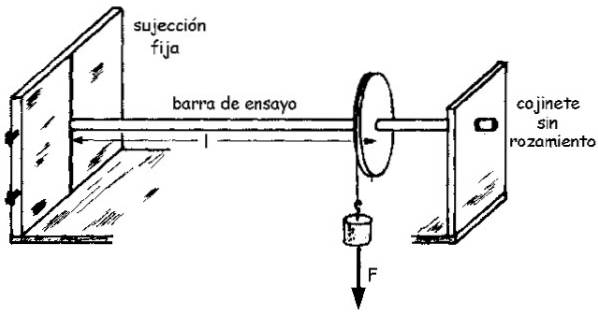
De omvang van het moment M., die we aanduiden als M. (niet vetgedrukt) is gerelateerd aan de geroteerde hoek θ door de afschuifmodulus G volgens de volgende vergelijking (afgeleid door een eenvoudige integraal):
Omdat de grootte van het moment gelijk is aan het product van de module van de kracht F en de straal van de katrol Rp
M = F.Rp
En kracht is het gewicht dat hangt W., dan:
M = W.Rp
Vervanging in de vergelijking voor de grootte van het moment:
Er is de relatie tussen gewicht en hoek:
Deze relatie tussen de variabelen W. Y θ is lineair, dus de verschillende hoeken die worden geproduceerd door verschillende gewichten op te hangen, worden gemeten.
De gewichts- en hoekparen worden uitgezet op ruitjespapier, de beste lijn die door de experimentele punten loopt, wordt gepast en de helling wordt berekend. m van genoemde lijn.
Aan één uiteinde is een staaf van 2,5 meter lang en een straal van 4,5 mm bevestigd. De andere is verbonden met een katrol met een radius van 75 cm die een hanggewicht W van 1,3 kg heeft. De gedraaide hoek is 9,5º.
Met deze gegevens wordt gevraagd om de afschuifmodulus G van de staaf te berekenen.
Uit de vergelijking:
G is gewist:
En de waarden die in de verklaring worden gegeven, worden vervangen, waarbij ervoor wordt gezorgd dat alle gegevens in het internationale systeem van eenheden SI worden uitgedrukt:
R = 4,5 mm = 4,5 x 10 -3 m
Rp = 75 cm = 0,075
Om van kilogram (wat eigenlijk kilogram is - kracht) naar newton te gaan, vermenigvuldig je met 9,8:
W = 1,3 kg-kracht = 1,3 x 9,8 N = 12,74 N
En tot slot moeten de graden in radialen zijn:
9,5 º = 9,5 x2π / 360 radialen = 0,1658 radialen.
Met dit alles heb je:
= 2237 x 1010 vader
Een kubus van gel heeft een zijde van 30 cm. Een van de vlakken is gefixeerd, maar tegelijkertijd wordt een parallelle kracht van 1 N uitgeoefend op het tegenoverliggende vlak, dat dankzij het 1 cm beweegt (zie het voorbeeld van het boek in figuur 1).
Er wordt gevraagd om met deze gegevens te rekenen:
a) De grootte van de schuifspanning
b) Stam δ
c) De waarde van de afschuifmodulus
De grootte van de schuifspanning is:
τ = F / A
Met:
A = kanttwee = (30 x 10-twee cm)twee = 0,09 mtwee
Daarom:
τ = 1 N / 0,09 mtwee = 11,1 Pa
Stam is niets anders dan de waarde van δ, gegeven door:
δ = Δx / L
De verplaatsing van het gezicht dat aan de kracht wordt blootgesteld, is 1 cm, dan:
8 = 1/30 = 0,0333
De afschuifmodulus is het quotiënt tussen de schuifspanning en de rek:
G = schuifspanning / rek
Daarom:
G = 11,1 Pa / 0,033 = 336,4 Pa
Niemand heeft nog op dit artikel gereageerd.