
Binominale stelling Bewijs en voorbeelden
De binomiale stelling is een vergelijking die ons vertelt hoe we een uitdrukking van de vorm kunnen ontwikkelen (a + b)n voor een natuurlijk getal n. Een binominaal is niets meer dan de som van twee elementen, zoals (a + b). Het stelt ons ook in staat om een term te kennen die wordt gegeven door eenkbn-k wat is de coëfficiënt die ermee gepaard gaat.
Deze stelling wordt gewoonlijk toegeschreven aan de Engelse uitvinder, natuurkundige en wiskundige Sir Isaac Newton; Er zijn echter verschillende gegevens gevonden die aangeven dat het bestaan ervan al rond het jaar 1000 bekend was in het Midden-Oosten.

Artikel index
- 1 Combinatorische nummers
- 2 Demo
- 3 voorbeelden
- 3.1 Identiteit 1
- 3.2 Identiteit 2
- 4 Nog een demonstratie
- 4.1 Bewijs door inductie
- 5 curiosa
- 6 referenties
Combinatorische nummers
De binominale stelling vertelt ons wiskundig het volgende:
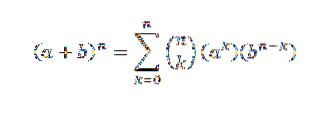
In deze uitdrukking zijn a en b reële getallen en is n een natuurlijk getal.
Laten we, voordat we de demo geven, eens kijken naar enkele basisconcepten die nodig zijn.
Het combinatorische getal of combinaties van n in k wordt als volgt uitgedrukt:
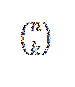
Dit formulier geeft de waarde weer van hoeveel subsets met k elementen kunnen worden gekozen uit een set van n elementen. De algebraïsche uitdrukking wordt gegeven door:
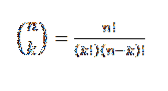
Laten we een voorbeeld bekijken: stel dat we een groep van zeven ballen hebben, waarvan er twee rood zijn en de rest blauw..
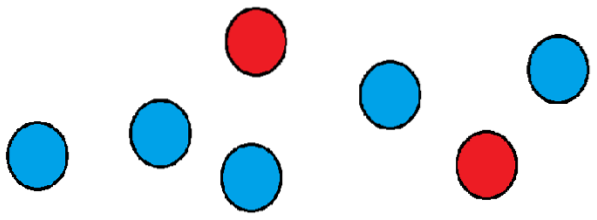
We willen weten op hoeveel manieren we ze op een rij kunnen ordenen. Een manier zou kunnen zijn om de twee rode ballen op de eerste en tweede positie te plaatsen en de rest van de ballen op de resterende posities..
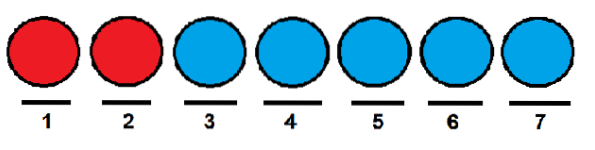
Net als in het vorige geval konden we de rode ballen respectievelijk de eerste en de laatste positie geven en de anderen bezetten met blauwe ballen.
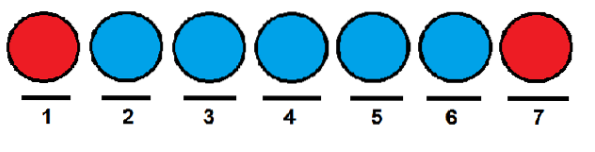
Een efficiënte manier om te tellen op hoeveel manieren we de ballen op een rij kunnen rangschikken, is door combinatorische getallen te gebruiken. We kunnen elke positie zien als een element van de volgende set:
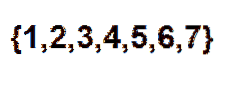
Dan blijft het alleen om een subset van twee elementen te kiezen, waarin elk van deze elementen de positie vertegenwoordigt die de rode ballen zullen innemen. We kunnen deze keuze maken op basis van de relatie die wordt gegeven door:
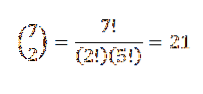
Op deze manier hebben we dat er 21 manieren zijn om deze ballen te bestellen.
Het algemene idee van dit voorbeeld zal erg nuttig zijn bij het bewijzen van de binominale stelling. Laten we naar een bepaald geval kijken: als n = 4, hebben we (a + b)4, wat niets meer is dan:
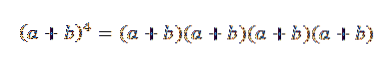
Wanneer we dit product ontwikkelen, houden we de som van de termen over die worden verkregen door een element van elk van de vier factoren (a + b) te vermenigvuldigen. We zullen dus termen hebben die de volgende vorm hebben:
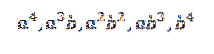
Als we de term wilden halen uit het formulier a4, vermenigvuldig gewoon als volgt:
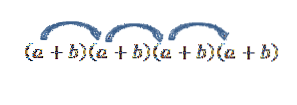
Merk op dat er maar één manier is om dit element te verkrijgen; maar wat gebeurt er als we nu zoeken naar de term van de vorm atweebtwee? Aangezien "a" en "b" reële getallen zijn en daarom de commutatieve wet geldig is, hebben we die ene manier om deze term te verkrijgen, is door te vermenigvuldigen met de leden zoals aangegeven door de pijlen.
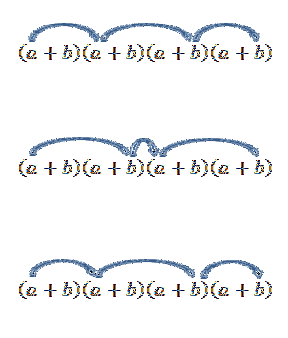
Het uitvoeren van al deze bewerkingen is meestal een beetje vervelend, maar als we de term 'a' zien als een combinatie waarbij we willen weten op hoeveel manieren we twee 'a' kunnen kiezen uit een reeks van vier factoren, kunnen we het idee van de vorig voorbeeld. We hebben dus het volgende:
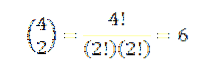
We weten dus dat in de laatste uitbreiding van de uitdrukking (a + b)4 we hebben precies 6atweebtwee. Als u hetzelfde idee gebruikt voor de andere elementen, moet u:
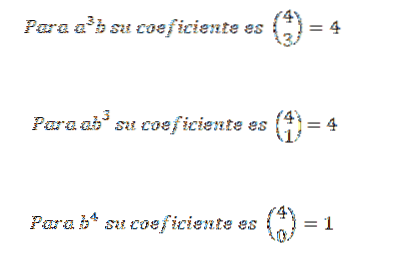
Vervolgens voegen we de eerder verkregen uitdrukkingen toe en we hebben dat:
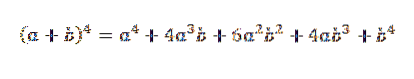
Het is een formeel bewijs voor het algemene geval waarin "n" een natuurlijk getal is.
Demonstratie
Merk op dat de termen die overblijven bij het ontwikkelen van (a + b)n Ze hebben de vorm akbn-k, waar k = 0,1, ..., n. Door het idee van het vorige voorbeeld te gebruiken, hebben we de manier om "k" variabelen te kiezen "a" van de "n" factoren is:
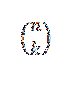
Door op deze manier te kiezen, kiezen we automatisch n-k variabelen "b". Hieruit volgt dat:
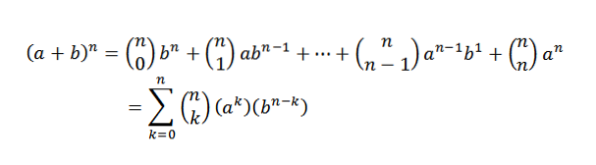
Voorbeelden
Gezien (a + b)5, Wat zou jouw ontwikkeling zijn?
Volgens de binominale stelling hebben we:
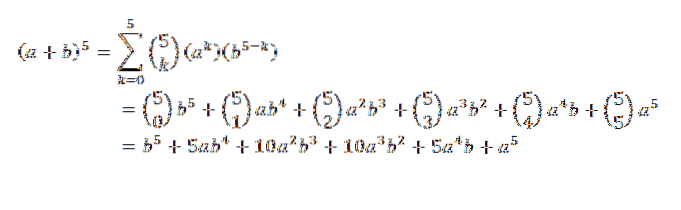
De binominale stelling is erg handig als we een uitdrukking hebben waarin we willen weten wat de coëfficiënt van een specifieke term is zonder de volledige expansie te hoeven doen. Als voorbeeld kunnen we de volgende onbekende nemen: wat is de coëfficiënt van x7Y9 in de uitbreiding van (x + y)16?
Volgens de binominale stelling hebben we dat de coëfficiënt is:
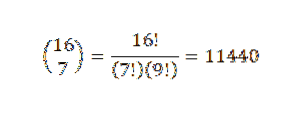
Een ander voorbeeld zou zijn: wat is de coëfficiënt van x5Y8 in de ontwikkeling van (3x-7j)13?
Eerst herschrijven we de uitdrukking op een gemakkelijke manier; dit is:
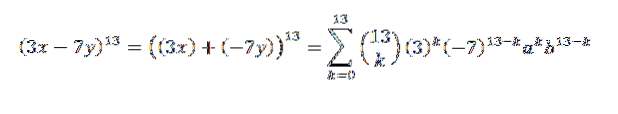
Vervolgens, met behulp van de binominale stelling, hebben we dat de gezochte coëfficiënt is wanneer we k = 5 hebben
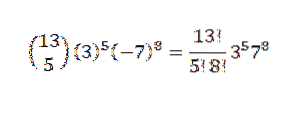
Een ander voorbeeld van het gebruik van deze stelling is het bewijs van enkele veelvoorkomende identiteiten, zoals degene die we hieronder zullen noemen.
Identiteit 1
Als "n" een natuurlijk getal is, hebben we:
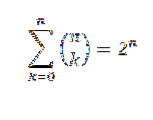
Voor het bewijs gebruiken we de binominale stelling, waarbij zowel "a" als "b" de waarde 1 hebben. Dan hebben we:
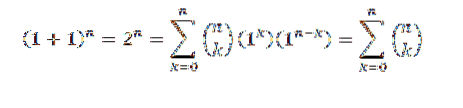
Op deze manier hebben we de eerste identiteit bewezen.
Identiteit 2
Als "n" een natuurlijk getal is, dan
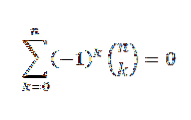
Volgens de binominale stelling hebben we:
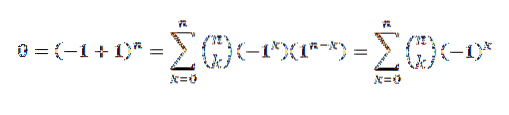
Nog een demonstratie
We kunnen een ander bewijs leveren voor de binominale stelling met behulp van de inductieve methode en de identiteit van Pascal, die ons vertelt dat, als 'n' en 'k' positieve gehele getallen zijn die voldoen aan n ≥ k, dan:
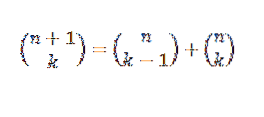
Inductiebestendig
Laten we eerst eens kijken of de inductieve basis klopt. Als n = 1, hebben we:
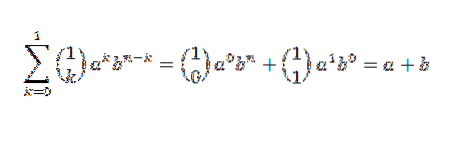
Inderdaad, we zien dat het is vervuld. Laat nu n = j zodanig zijn dat:
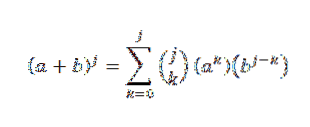
We willen zien dat voor n = j + 1 het waar is dat:
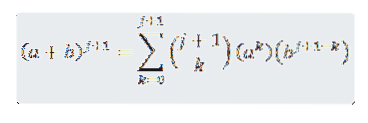
We moeten dus:
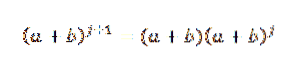
Door hypothese weten we dat:
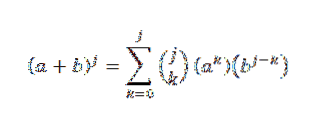
Gebruik vervolgens de distributieve eigenschap:
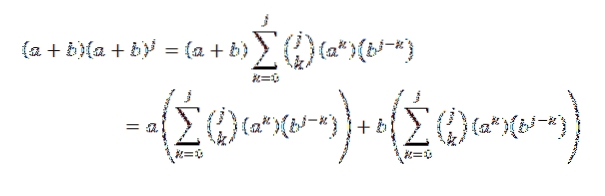
Vervolgens hebben we bij het ontwikkelen van elk van de sommaties:
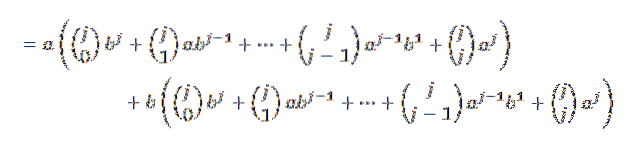
Als we nu op een gemakkelijke manier groeperen, hebben we dat:
Met behulp van de identiteit van pascal hebben we:
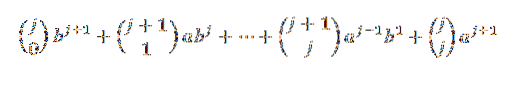
Merk ten slotte op dat:
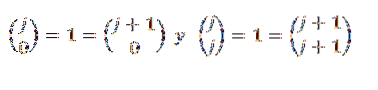
Daarom zien we dat de binominale stelling geldt voor alle "n" die tot de natuurlijke getallen behoren, en daarmee eindigt het bewijs.
Curiosa
Het combinatorische getal (nk) wordt ook wel de binominale coëfficiënt genoemd omdat het precies de coëfficiënt is die verschijnt in de ontwikkeling van de binominale (a + b)n.
Isaac Newton gaf een generalisatie van deze stelling voor het geval waarin de exponent een reëel getal is; deze stelling staat bekend als de binominale stelling van Newton.
Al in de oudheid was dit resultaat bekend voor het specifieke geval waarin n = 2. Dit geval wordt vermeld in het Elementen door Euclid.
Referenties
- Johnsonbaugh Richard. Discrete wiskunde. PHH
- Kenneth.H. Rosen Discrete wiskunde en haar toepassingen. S.A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Seymour Lipschutz Ph.D & Marc Lipson. Discrete wiskunde. McGRAW-HILL.
- Ralph P. Grimaldi. Discrete wiskunde en combinatoriek. Addison-Wesley Iberoamericana
- Verde Star Luis… Discrete en combinatorische wiskunde.Anthropos


Niemand heeft nog op dit artikel gereageerd.