
Formulewerk, eenheden, voorbeelden, oefeningen

De baan In de natuurkunde is het de overdracht van energie die wordt uitgevoerd door een kracht wanneer het object waarop het inwerkt, beweegt. Wiskundig neemt het de vorm aan van het scalaire product tussen de krachtvectoren F. en verplaatsing s.
En aangezien het scalaire product tussen twee loodrechte vectoren nul is, komt het voor dat de krachten die 90º vormen met de verplaatsing niet werken volgens de definitie, aangezien:
W = F. s = F⋅ s⋅ cos θ
Waar W staat voor werk, van het Engelse woord werk.
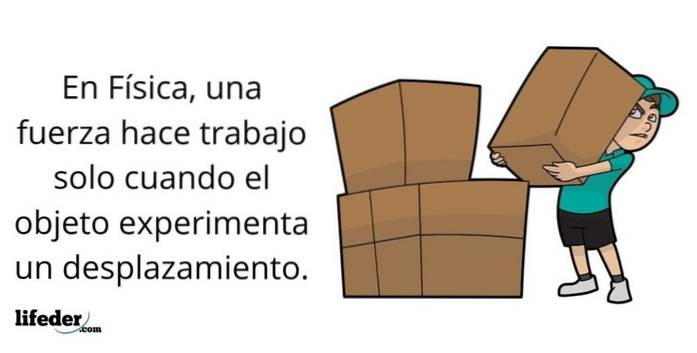
Het voordeel van het definiëren van het werk is dat het een scalair is, dat wil zeggen dat het geen richting of zin heeft, alleen module en de respectieve eenheid. Dit maakt het gemakkelijker om berekeningen uit te voeren met energieveranderingen veroorzaakt door de werking van krachten..
Zwaartekracht en kinetische wrijving zijn voorbeelden van krachten die vaak werken op bewegende objecten. Een andere veel voorkomende kracht is de normale uitgeoefende door een oppervlak, maar in tegenstelling tot deze, werkt het nooit op objecten, omdat het loodrecht op de verplaatsing staat..
Wanneer een lichaam vrij valt, doet de zwaartekracht positief werk op de mobiel, waardoor het sneller wordt als het valt. Aan de andere kant heeft kinetische wrijving een volledig tegenovergesteld effect, omdat het, omdat het altijd tegen beweging is, negatief werk verricht dat het niet bevordert..
Artikel index
- 1 Formules en bijzondere gevallen
- 1.1 Werk verricht door variabele krachten
- 2 werkeenheden
- 2.1 Eenheden in het Britse systeem
- 2.2 Andere eenheden voor werk
- 3 Voorbeelden van werk
- 3.1 Opstijgen en dalen van objecten
- 3.2 Puntladingen in elektrische velden
- 3.3 Wrijving tussen oppervlakken
- 3.4 Duwen en trekken
- 3.5 Kracht in een katrol
- 3.6 Normaalkrachten of steunen
- 3.7 Magnetische kracht
- 3.8 Objecten vastgebonden aan een touw
- 3.9 Satellieten in een baan om de aarde
- 3.10 Massaveersysteem
- 4 Oefening opgelost
- 5 referenties
Formules en bijzondere gevallen
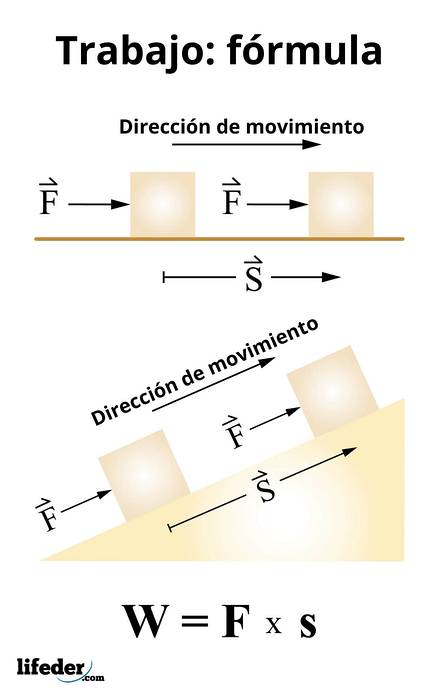
Het werk wordt berekend door:
W = F. s
Deze uitdrukking is geldig voor constante krachten en volgens de definitie van een scalair product is het gelijk aan:
W = F. s. cos θ
Waar θ de hoek is tussen de kracht en de verplaatsing. Hieruit volgt dat alleen die krachten die een component in de verplaatsingsrichting hebben, aan een lichaam kunnen werken.
En ook wordt duidelijk dat als er geen beweging is, er ook geen werk is.
Wat het teken betreft, het werk kan positief, negatief of nul zijn. Als de kracht een component heeft die parallel is aan de beweging, hangt het teken van het werk af van de waarde van cos θ.
Er zijn enkele bijzondere gevallen die het overwegen waard zijn:
- Wanneer de kracht parallel is aan de verplaatsing, is de hoek daartussen F. Y s is 0º, daarom is het werk van de kracht positief en de waarde is maximaal:
W = F⋅s cos 0º = F⋅s
- Als de kracht de verplaatsing tegenwerkt, dan is de hoek daartussen F. Y s is 180º, het werk van F is negatief en minimaal:
W = F⋅s cos 180º = -F⋅s
- Ten slotte is er het eerder genoemde geval: als de hoek gevormd door F. Y s is 90º, aangezien cos 90º = 0, is het werk nul:
W = F⋅s cos 90º = 0
Werk gedaan door variabele krachten
Soms is de uitgeoefende kracht niet constant; in dat geval moet u uw toevlucht nemen tot berekeningen om het uitgevoerde werk te vinden. Eerst wordt een arbeidsverschil dW bepaald, uitgevoerd op een oneindig kleine verplaatsing ds
dW = F⋅ds
Om de waarde te vinden van het totale werk dat door deze kracht wordt gedaan wanneer het object van punt A naar punt B gaat, is het nodig om beide zijden als volgt te integreren:
Werkeenheden
De eenheid voor werk in het internationale systeem is de joule, afgekort J. De eenheid ontleent zijn naam aan de Engelse natuurkundige James Prescott Joule, een pionier in de studie van thermodynamica..
Uit de werkvergelijking wordt de joule gedefinieerd als 1 newton per meter:
1 J = 1 N⋅m
Eenheden in het Britse systeem
Werk komt overeen als een eenheid pondkracht x voet, soms bellen pond-kracht voet. Het is ook een eenheid voor energie, maar er moet aan worden herinnerd dat werk dat aan een lichaam wordt gedaan, zijn energietoestand verandert en dat daarom werk en energie gelijkwaardig zijn. Geen wonder dat ze dezelfde schijven hebben.
De gelijkwaardigheid tussen de pondkrachtvoet en de joule is als volgt:
1 foot-pound-force = 1.35582 J
Een bekende eenheid voor werk en energie, vooral op het gebied van koeling en airconditioning is de BTU of Britse Warmte-eenheid.
1 BTU is gelijk aan 1055 J en 778.169 foot-pound-force.
Andere eenheden voor werk
Er zijn andere eenheden voor werk die worden gebruikt in specifieke gebieden van natuurkunde en techniek. Onder hen hebben we:
Erg
Aangeduid als erg, is de werkeenheid in het cegesimale systeem en is gelijk aan 1 dyna⋅cm of 1 x 10-7 J.
Electron-volt
Afgekort eV, het wordt vaak gebruikt in de deeltjesfysica en wordt gedefinieerd als de energie die een elektron verwerft wanneer het door een potentiaalverschil van 1 V beweegt.
Kilowattuur (kWh)
Het verschijnt vaak op rekeningen van nutsbedrijven. Het is het werk dat gedurende 1 uur wordt uitgevoerd door een bron met een vermogen van 1 kW, wat overeenkomt met 3,6 x 106 J.
Calorie
Het is meestal gerelateerd aan de energie van voedsel, hoewel in deze context in feite wordt verwezen naar een kilocalorie, dat wil zeggen, 1000 calorieën. Eigenlijk zijn er meerdere units die deze naam krijgen, dus de context moet heel goed gespecificeerd worden.
De gelijkwaardigheid tussen de joule en 1 thermochemische calorie het is:
1 calorie = 4,1840 J.
Werkvoorbeelden
Opstijgen en dalen van objecten
Wanneer lichamen afdalen, hetzij verticaal, hetzij langs een helling, doet het gewicht positief werk en bevordert het beweging. In plaats daarvan, wanneer een object opstijgt, doet de zwaartekracht negatief werk.
Puntladingen in elektrische velden
Een uniform elektrisch veld werkt op een puntlading die erin beweegt. Afhankelijk van het veld en het teken van de lading, kan dit werk negatief of positief zijn.
Wrijving tussen oppervlakken
Kinetische wrijving tussen oppervlakken doet altijd negatief werk op het bewegende object.
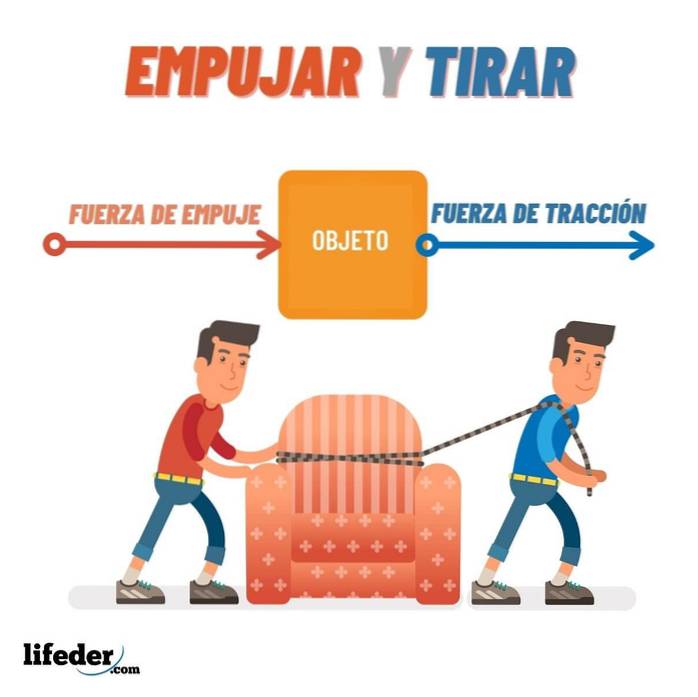
Duwen en trekken

Duwen is een kracht die een voorwerp ergens vandaan trekt. Trekken is een kracht die ervoor zorgt dat een object zichzelf dichterbij brengt.
Forceer een katrol
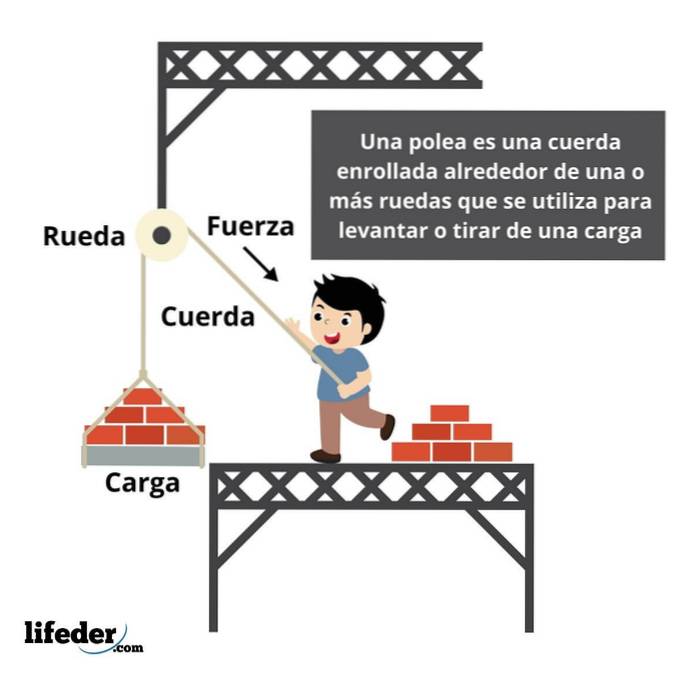
Een katrol is een systeem dat wordt gebruikt om een kracht over te brengen vanaf een van zijn uiteinden. In een eenvoudige katrol moet, om de last op te tillen, een kracht worden uitgeoefend die gelijk is aan de weerstand die door het object wordt uitgeoefend.
Normale krachten of steunen
De normale, zoals hierboven opgemerkt, werkt nul wanneer een object dat op een oppervlak rust erop beweegt, zelfs als het oppervlak niet vlak is of als het schuin staat..
Magnetische kracht
Een andere kracht die nul werk doet, is de magnetische kracht die een uniform veld uitoefent op het geladen deeltje dat er loodrecht op staat. De beweging van het deeltje blijkt een uniforme cirkelvormige beweging te zijn, met de kracht in radiale richting. Omdat de verplaatsing loodrecht op de kracht staat, werkt deze niet op de last..
Objecten vastgebonden aan een touw
Een touw werkt ook niet op een hangende slinger, aangezien de spanning erin altijd loodrecht staat op de verplaatsing van de massa..
Satellieten in een baan
De zwaartekracht werkt ook niet op een satelliet in een cirkelvormige baan, om dezelfde reden als de vorige gevallen: het staat loodrecht op de verplaatsing..
Massa-veersysteem
In een massa-veersysteem is de kracht F. dat de veer op de massa oefent, heeft een omvang F = kx, waar k is de veerconstante en X zijn compressie of verlenging. Het is een variabele kracht, daarom hangt het werk af van hoeveel de veer uitrekt of krimpt.
Oefening opgelost
De volgende grafiek toont het werk dat wordt gedaan door een variabele kracht F.X die afhangt van de positie X. Dit is de kracht die wordt uitgeoefend door een hamer op een spijker. Het eerste deel is de kracht die wordt gebruikt om op het zachtere deel van de muur te spijkeren en het tweede om de spijker af te slaan.
Hoeveel werk moet de hamer doen om de spijker in totaal 5 cm in de muur te laten zakken?
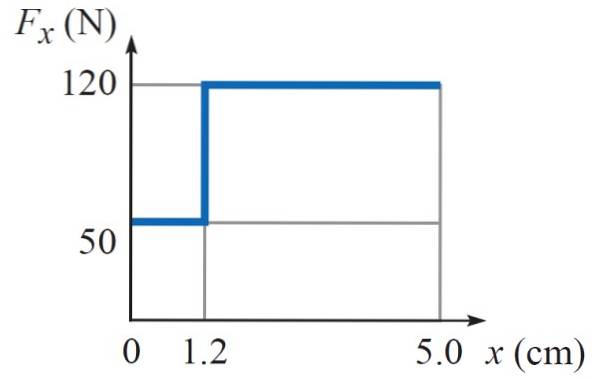
Oplossing
De kracht die door de hamer wordt uitgeoefend, is variabel, aangezien er minder intensiteit (50 N) nodig is om de nagel 1,2 cm in het zachte deel van de muur te slaan, terwijl het in het hardere deel 120 N kost om de nagel te laten zakken tot 5 cm diep, zoals weergegeven in de tabel.
In dit geval is het werk de integraal:

Waar A = 0 cm en B = 5 cm. Aangezien de integraal het gebied onder de grafiek Fx vs x is, volstaat het om dit gebied te vinden, dat overeenkomt met twee rechthoeken, de eerste met hoogte 50 N en breedte 1,2 cm, en de tweede met hoogte 120 N en breedte (5 cm - 1,2 cm) = 3,8 cm.
Beide worden berekend en opgeteld om het totale werk te geven:
B = 50 N x 1,2 cm + 120 N x 3,8 cm = 516 N. cm = 516 N x 0,01 m = 5,16 J.
Referenties
- Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 2. Dynamiek. Bewerkt door Douglas Figueroa (USB).
- Giambattista, A. 2010. Physics. 2e. Ed McGraw Hill.
- Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. Ed. Deel 1. Pearson.
- Serway, R., Jewett, J. (2008). Physics for Science and Engineering. Deel 1. 7e. Ed. Cengage Learning.
- Zapata, F. Mechanisch werk. Hersteld van: francesphysics.blogspot.com.



Niemand heeft nog op dit artikel gereageerd.